Research

My research centers on uncertainty quantification, machine learning, and scientific computing. During my postdoc, I developed a new method for choosing the basis functions for Dynamic Mode Decomposition (a reduced-order modeling technique). I also worked on model structural inference and uncertainty quantification for dynamical systems. At Brookhaven, I focus on applying methods from machine learning and uncertainty quantification to the design of optimal experiments and to the automation of data processing. I led a project on using encoder-decoder neural networks to automatically denoise data from X-Ray Photon Correlation spectroscopy (XPCS) data. I am currently working on applying Bayesian inference to calibrate computational models in materials science to data.
You may find a list of my publications on my Google scholar page.
Cahn Hilliard templating effect

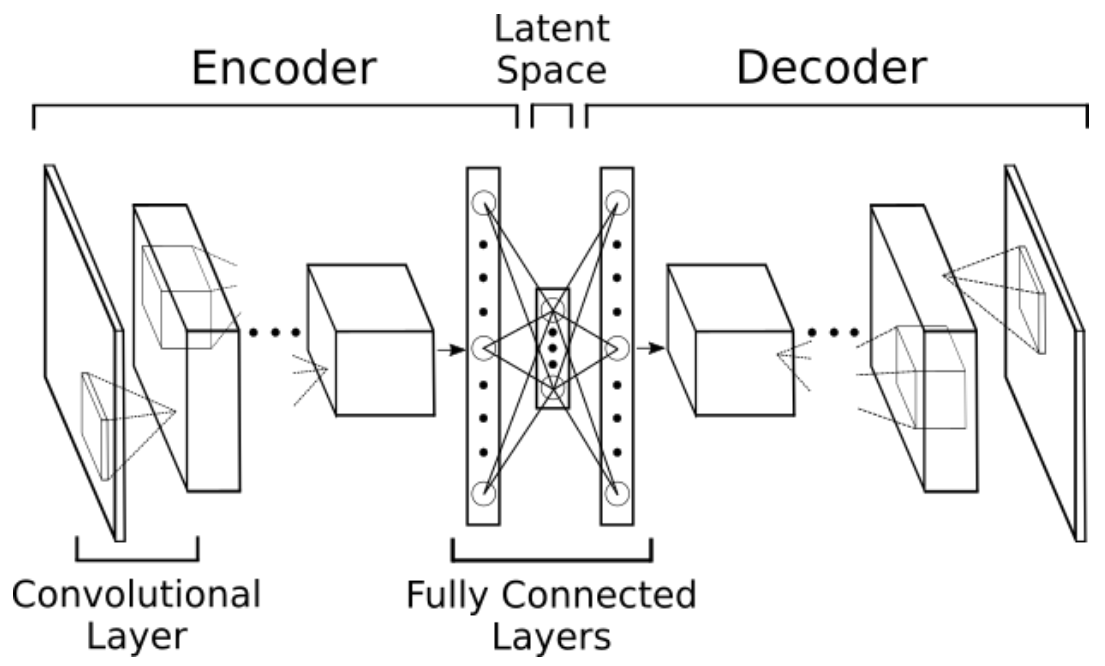Encoder-decoder neural network used in XPCS data denoising. 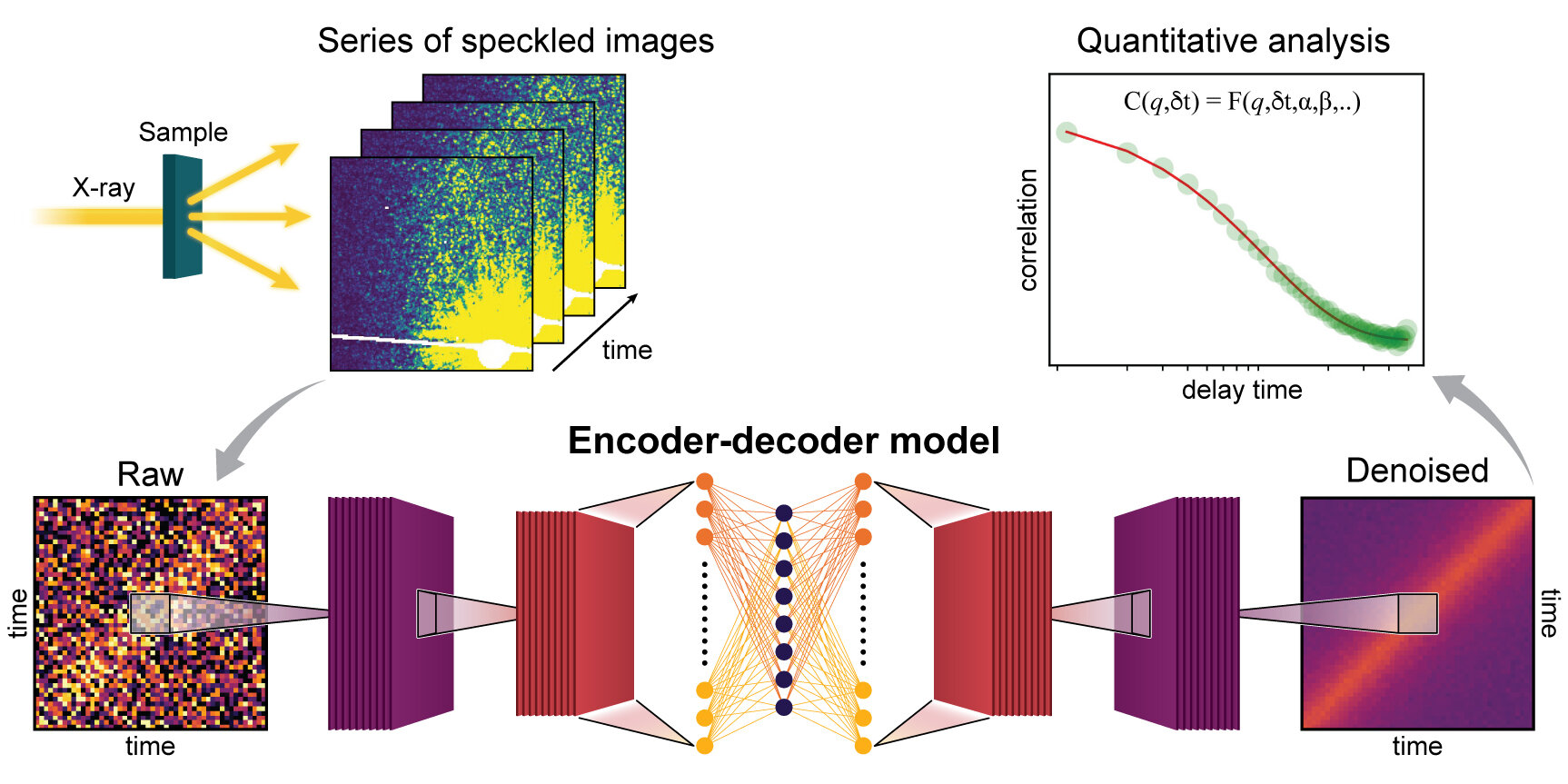Encoder-decoder neural network used in XPCS data denoising.

Machine learning for automated experimental data processing

Encoder-decoder neural network and XPCS sample data and analysis (credit: Brookhaven National Laboratory). For details, see Konstantinova et al. 2020, Scientific Reports and Konstantinova et al. 2021, Physical Review Research.
X-Ray Photon Correlation Spectroscopy (XPCS) is an experimental technique that allows one to measure the dynamics of a material sample. As an experimental technique, the data produced from this method is corrupted by noise, which must be removed as the first step of an analysis. While this is possible, it traditionally requires a certain amount of human intervention to perform, and this has become a "bottleneck" which limits the pace of materials discovery.
Fortunately, computer vision methods borrowed from machine learning (ML) provide a way to resolve this issue in an automated way. To do so, we trained encoder-decoder neural networks in a supervised setting on datasets consisting of previously observed experimental data. The input data was a noise-corrupted two-time correlation function, and the output was a denoised version of the same correlation function. We were able to demonstrate positive results of this procedure on equilibrium and quasi-equilibrium data, as well as on some forms of non-equilibrium data.

Uncertainty quantification for block copolymer design

Simulation of thin-film BCP self-assembly in Cahn Hilliard.
Block copolymer (BCP) systems are of tremendous interest to scientists and engineers alike. From a theoretical point-of-view, they offer a glimpse at how complex, multiscale phenomena may develop through self-assembly. From an engineering point-of-view, the ability to direct/control the nanoscale structure of these materials may have relevance to battery design and semiconductor manufacturing.
We have developed an extension to the Discontinuous Galerkin code Madgicart, which allows us to compute solutions to the 3D nonlocal Cahn Hilliard equations. This code is written in C++, runs on a single GPU, and is containerized for portability using Docker and Singularity. Petsc is a notable third-party library used, which grants us easy access to implicit timestepping methods and various preconditioners.
We are currently researching how "realistic" parameter values for the Cahn Hilliard equations may be inferred from experimental data, using Bayesian methods. Doing so will enable fast prediction of exotic material designs and associated parameter sweeps that are currently too computationally prohibitive to perform.